 | Jeremiah Day - Measurement - 1815 - 388 pages
...the opposite angles, !Ło the tangent of half their difference. Thus the sum of AB and AC (Fig. 25.) is to their difference ; as the tangent of half the sum of the angles ACB and ABC, to the tangent of half their difference. Demonstration. Extend CA to G, making... | |
 | Euclides - 1816 - 588 pages
...in a plane triangle, any three being given, the fourth is also given. PROP. III. FIG. 8. IN a plane triangle, the sum of any two sides is to their difference, as the tangent of half the sum of the angles at the base, to the tangent of half their difference. . Let ABC be a plane triangle, the sum... | |
 | Olinthus Gregory - Plane trigonometry - 1816 - 276 pages
...cosines being the sines of the complements, it follows from the proposition that the sum of the cosines, is to their difference, as the tangent of half the sum of the complements, is to the tangent of halt' their difference. But half the sum of the complements of two... | |
 | Sir John Leslie - Geometry - 1817 - 456 pages
...cos la + 7 cos5a + 21 cos3a + 35c. ' &e. &c. &c. PROP. IV. THEOR. The sum of the sines of two arcs is to their difference, as the tangent of half the sum of those arcs to the tangent of half the difference. If A and B denote two arcs ; smA+«'wB : sin A—... | |
 | Miles Bland - Euclid's Elements - 1819 - 444 pages
...found*. * The preceding expressions not being easy for calculation, values i . may PROP. XIII. (88.) In any triangle, the sum of any two sides is to their difference as the tangent of the semi-sum of the angles at the base is to the tangent of their semi-difference. Let ABC be any triangle,... | |
 | Thomas Leybourn - Mathematics - 1819 - 430 pages
...: BC* : AC*. Required a proof. 8. Prove, geometrically, that in any plane triangle, the sum of the sides is to their difference as the tangent of half the sum of the angles at the base to the tangent of half their difference. 9. Shew that tan.3 60 = 3 tan. 60 to rad.... | |
 | John Playfair - Circle-squaring - 1819 - 350 pages
...the difference between either of them and 45o. * PROP. IV. The sum of any troo sides of a triangle is to their difference, as the tangent of half the sum of the angles opposite to those sides, to the tangent of half their difference. Let ABC be any plane triangle... | |
 | Adrien Marie Legendre - Geometry - 1822 - 394 pages
...principles of Art. 42 and 43 are easily deducible. XL VII. In any rectilineal triangle, the sum of two sides is to their difference, as the tangent of half the sum of the angles opposite those sides is to the tangent of half the difference of those same angles. From the... | |
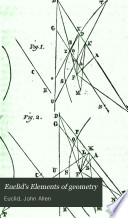 | Rev. John Allen - Astronomy - 1822 - 516 pages
...legs AC and CB, and AD their difference ; therefore the sum of the legs AC, CB of the triangle ABC is to their difference, as the tangent of half the sum of the angles CAB and CBA at the Ijase is tQ the tangent of half their difference. PROP. VII. THEOR. If to... | |
 | Peter Nicholson - Architecture - 1823 - 210 pages
...BC : : AC - BC : AD - BD. TRIGONOMETRY. — THEOREM 2. 234. The sum of the two sides of a triangle is to their difference as the tangent of half the sum of the angles at the base is to the tangent of half their difference. Let ABC be a triangle ; then, of the... | |
| |
In every plane triangle, the sum of two sides is to their difference as the tangent of half the sum of the angles opposite those sides is to the tangent of half their difference. 
